usehook - 前端码易

code deep_

所有专栏

免费领 30 美元额度

创建时间: 2025-04-16最后更新: 2025-12-22作者: yangbo(96862973d)

NOTE

请勿第一时间看答案, 先自己思考, 思考不出来, 再看答案

练习题：二叉树的后续遍历

原题地址：145. 二叉树的后序遍历

题目描述：

给你一棵二叉树的根节点 root , 返回其节点值的后序遍历数组.

二叉树的三种遍历方法的考查顺序一致, 只是输出顺序不一样：

前序遍历：遍历到一个节点后, 即刻输出该节点的值, 并继续遍历其左右子树. 输出顺序：根、左、右

中序遍历：遍历到一个节点后, 将其暂存, 遍历完左子树后, 再输出该节点的值, 然后遍历右子树. 输出顺序：左、根、右

后序遍历：考察到一个节点后, 将其暂存, 遍历完左右子树后, 再输出该节点的值. 输出顺序：左、右、根

示例1：

index.ts

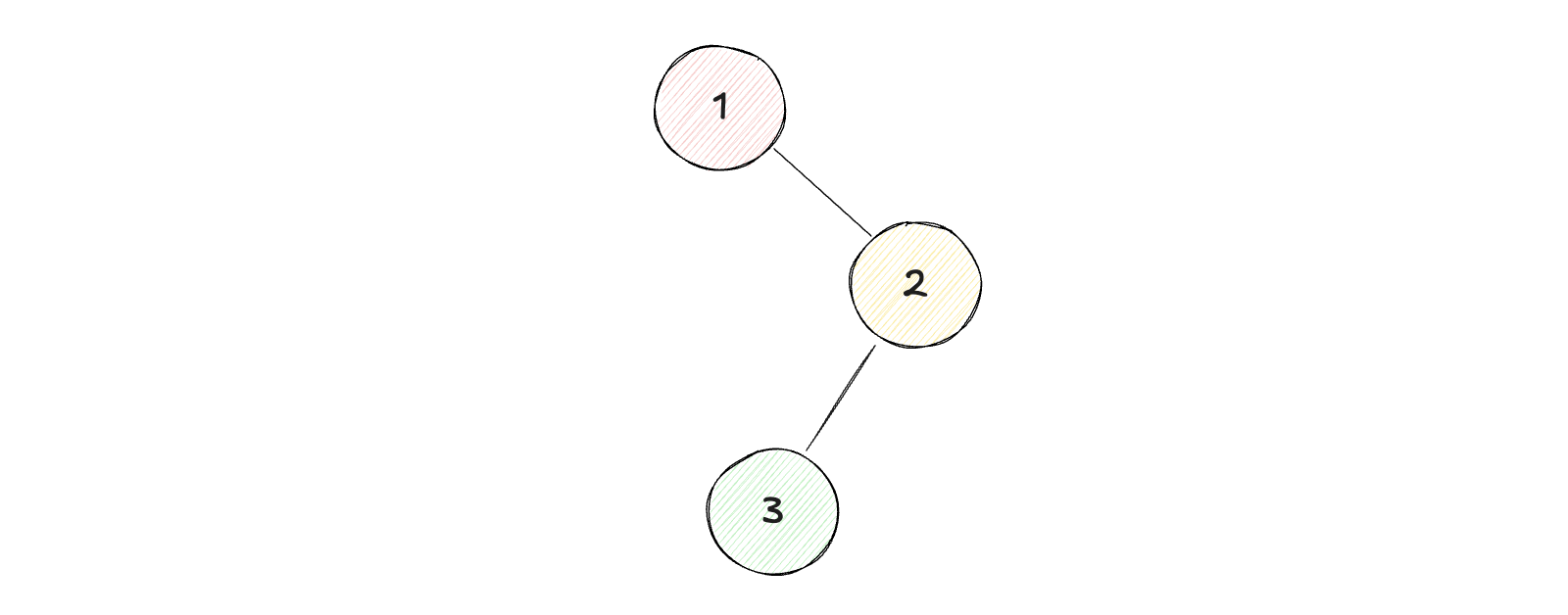
1输入：root = [1, null, 2, 3]
2输出：[3, 2, 1]

示例2：

index.ts

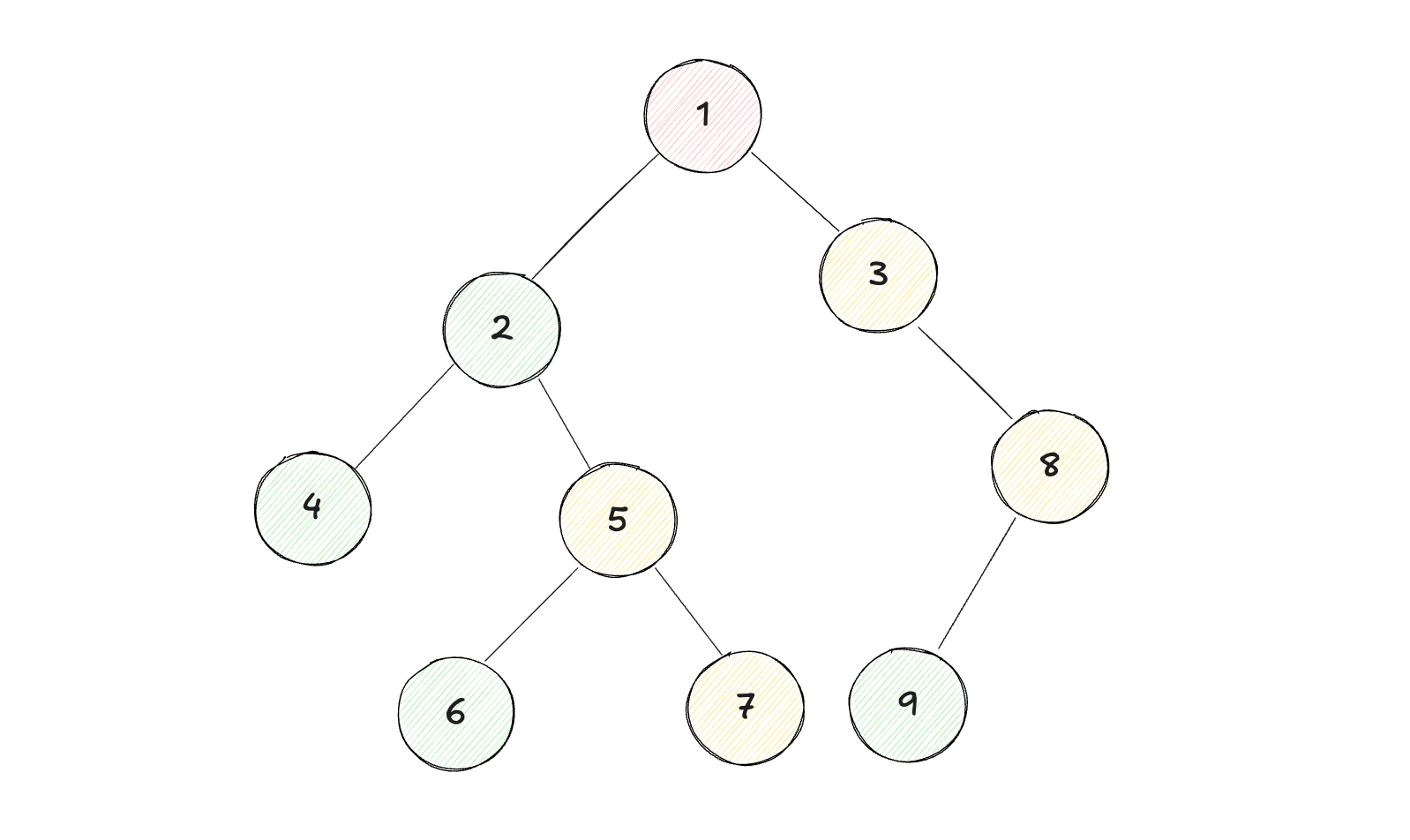
1输入：root = [1, 2, 3, 4, 5, null, 8, null, null, 6, 7, 9]
2输出：[4, 6, 7, 5, 2, 9, 8, 3, 1]

解题思路

语法基础 -> 8、迭代

在迭代章节中, 我们学习了使用栈来模拟递归的过程. 因此, 无论是前序遍历、中序遍历还是后序遍历, 我们都可以使用栈来实现. 并且执行的过程都是一样的, 只是输出顺序不同

因此, 我们首先依然是定义一个栈数组, 用于帮助使用迭代来模拟栈的顺序, 然后定义一个结果数组, 用于存储输出结果

index.ts

1const stack: TreeNode[] = []
2const res: number[] = []

然后需要按照栈的循序依次将节点压入栈中, 在判断到节点没有任何子节点之后, 再弹出栈中.

index.ts

01const stack = []
02// 将根节点压入栈中
03stack.push(root)
04root.x = true // 标记节点是否已经访问过
05// 遍历栈, 遍历的结束条件为栈数组被清空
06while(stack.length !== 0) {
07  const top = stack[stack.length - 1]
08  
09  // 先左边入栈、再右边入栈
10  if (top.left && !top.left.x) {
11    stack.push(top.left)
12    top.left.x = true
13  } else if (top.right && !top.right.x) {
14    stack.push(top.right)
15    top.right.x = true
16  } else {
17    // 如果节点没有任何子节点, 则弹出栈中
18    stack.pop()
19  }
20}

记录了执行过程之后, 表示每个节点实际上我们都执行到位了, 我们接下来需要做的就是在合适的时候, 把对应的节点值记录到结果数组中. 先序是在入栈的时候记录, 而后序则是在节点出栈的时候记录.

所以, 最终完整的代码如下所示

answer1.ts

01class TreeNode {
02  val: number
03  left: TreeNode | null
04  right: TreeNode | null
05  constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
06    this.val = (val===undefined ? 0 : val)
07    this.left = (left===undefined ? null : left)
08    this.right = (right===undefined ? null : right)
09 }
10}
11
12function preorderTraversal(root) {
13  const res = []
14  if (!root) {
15    return res
16  }
17  // 定义栈数组
18  const stack = []
19  // 将根节点压入栈中
20  stack.push(root)
21  root.x = true // 标记节点是否已经访问过
22  // 遍历栈, 遍历的结束条件为栈数组被清空
23  while(stack.length !== 0) {
24    const top = stack[stack.length - 1]
25    
26    if (top.left && !top.left.x) {
27      stack.push(top.left)
28      top.left.x = true
29    } else if (top.right && !top.right.x) {
30      stack.push(top.right)
31      top.right.x = true
32    } else {
33      const node = stack.pop()
34      res.push(node.val)
35    }
36  }
37
38  return res
39};

我的这种思路是严格按照栈的思路来解决的, 所以代码比较中规中矩. 但是我们可以通过魔改入栈的顺序来简化代码, 不过这会带来理解上的困难. 其他方式大家可以参考评论区, 我这里就不再赘述.

例如, 下面这种解法, 通过定义一个 current 指针来记录当前节点, 在逻辑的控制上, current 指针的移动顺序与栈的顺序一致, 然后通过 lastNode 来记录上一次出栈的节点, 从而判断当前节点是否有右节点, 有则压栈, 否则记录节点信息并出栈.

同样在出栈时, 按照后序遍历的顺序来记录节点信息.

answer2.ts

01var postorderTraversal = function(root) {
02  const stack = []
03  let current = root
04  let lastNode = null
05  let result = []
06  while(stack.length || current){
07    // 压入当前节点
08    if(current){
09      stack.push(current)
10      current = current.left
11    }else{
12      const node = stack[stack.length-1]
13      // 取栈顶的节点,判断是否有右节点, 有则压栈(注意是否已经遍历过了)
14      if(node.right&&node.right !== lastNode) {
15        current = node.right
16      } else {
17      // 记录节点信息并且出栈
18        result.push(node.val)
19        lastNode = stack.pop()
20      }
21    }
22  }
23  return result
24};

专栏首页

到顶

专栏目录