usehook - 前端码易

code deep_

所有专栏

免费领 30 美元额度

创建时间: 2025-04-14最后更新: 2025-12-22作者: yangbo(96862973d)

基础概念

从语义上来说, 迭代指的是针对同一段逻辑的重复执行, 不断利用变量的旧值, 计算出新值的过程. for 循环就是最常见的迭代形式之一.

从开发思维上来说, 迭代与递归, 是在运用同样的思维来解决问题. 他们只是在语法上体现得不一样.

在语法上, 递归强调的是调用自身, 而迭代强调的是循环.

但是在开发思维上, 递归强调的是

找到规律
找到递过程的终止条件, 也就是归过程的开始条件

迭代强调的是

找到规律
找到迭代的开始条件, 也就是递过程的终止条件
找到循环的终止条件

这里的区别就是, 递归是利用调用自身的方式, 由程序员自己通过递的过程, 找到逻辑执行的开始条件. 此时说的是归执行的开始条件.

迭代是开发者通过自己的思考, 找到逻辑执行的开始条件, 然后通过循环的方式执行到结束条件.

以斐波那契数列为例, 我们来看一下递归和迭代的区别.

斐波那契数列指的是, 从第三项开始, 当前项等于前面两项的总和. 所以使用数学公式表示为：

index.ts

1F(0) = 0
2F(1) = 1
3F(n) = F(n-1) + F(n-2)

那么递归的思路就是从入参自上而下的拆解问题, 直到找到终止条件.

code.ts

1function fib(n: number): number {
2  if (n === 0) {
3    return 0
4  }
5  if (n === 1) {
6    return 1
7  }
8  return fib(n - 1) + fib(n - 2)
9}

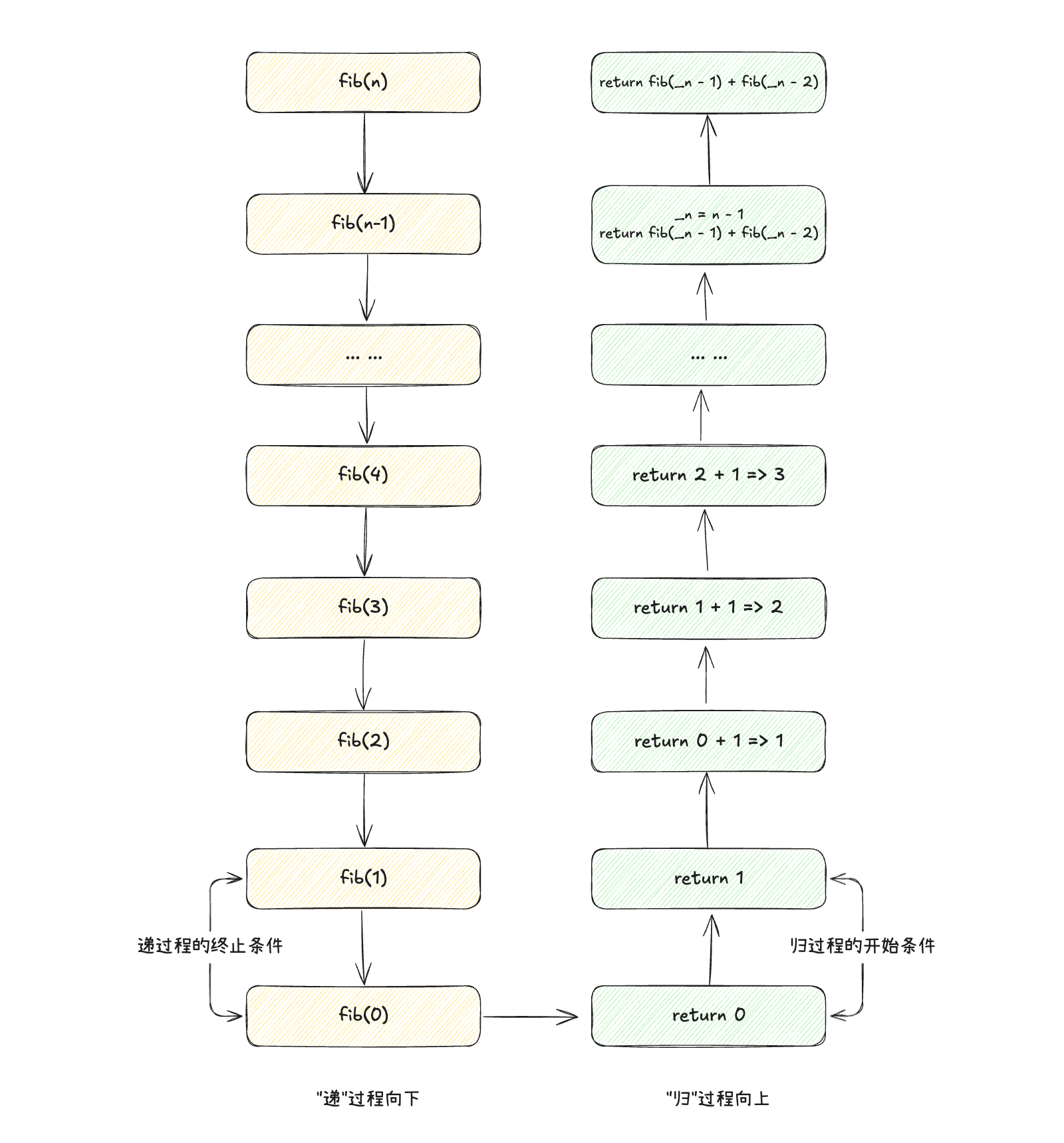
迭代的思维就是, 当我们已经找到了逻辑执行的开始条件, 那么我们就可以直接利用循环来直接执行逻辑.

在迭代执行的过程中, 我们会定义迭代值, 用于记录上一次迭代的执行结果. 然后利用循环来不断更新迭代值.

code.ts

01function fib(n: number): number {
02  if (n === 0) {
03    return 0
04  }
05  if (n === 1) {
06    return 1
07  } 
08  // 记录迭代值
09  let a = 0 // 表示当前值的前两项
10  let b = 1 // 表示当前值的前一项
11  for (let i = 2; i <= n; i++) {    
12    // 计算当前项的值
13    const temp = a + b
14    // 更新迭代值
15    a = b
16    b = temp
17  }
18  return b
19}

从解题思路上来说, 迭代是在递归思维的归过程上, 利用循环来不断更新迭代值, 从而得到最终结果. 如下图所示

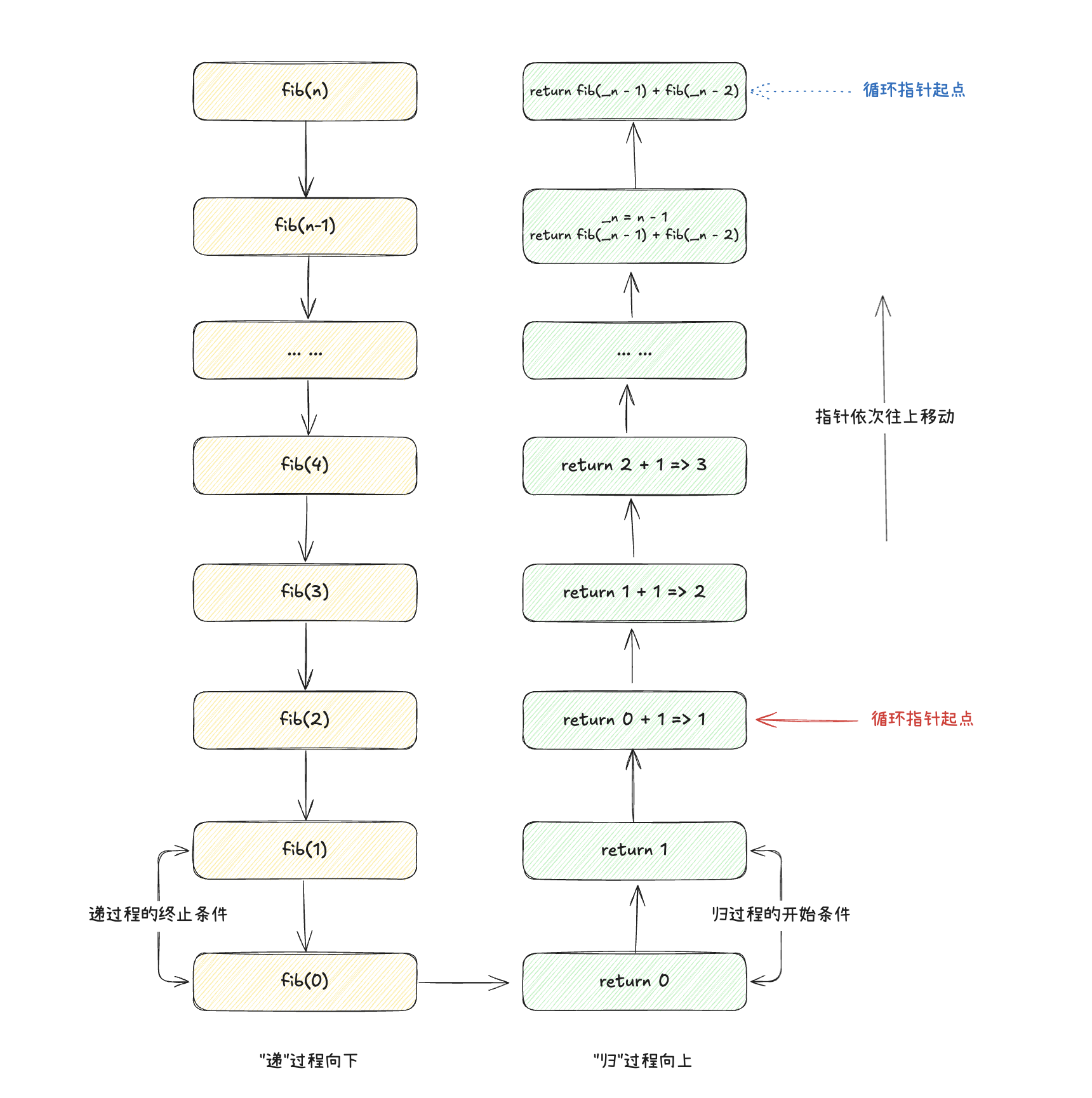
从这个案例中, 我们可以看出, 递归思维是自上而下的拆解问题并解决, 而迭代思维是自下而上的解决问题. 递归思维利用程序的调用栈执行机制, 自动找到归过程的开始条件, 而迭代思维需要我们自己找到逻辑执行的开始条件.

递归思维利用程序的调用栈来保存每一次的执行结果, 而迭代思维利用循环来不断更新迭代值, 从而得到最终结果.

通常情况下, 通过递归来解决问题的思考过程会比迭代更简单. 但是执行效率会低一些. 在实践开发中, 如果我们可以通过自己的思考找到逻辑执行的开始条件, 那么我们通常会优先使用迭代来解决这个问题, 没办法找到, 则使用递归

所以, 递归思维更侧重于对问题进行分治拆解. 迭代思维更侧重于对问题的解决方案上执行效率的提升. 我们可以把他们看成是同一种思维, 许多场景下他们的代码都可以相互转化, 也可以综合利用他们的思路来解决复杂问题, 我们后续会根据场景的不同学习分治、动态规划等策略, 都是基于这两种思维的.

练习题：二叉树的前序遍历

原地地址：144. 二叉树的前序遍历

题目描述：

给你二叉树的根节点 root, 返回它节点值的前序遍历数组.

二叉树的前序遍历顺序是在深度优先遍历的基础之上：

先访问根节点
然后访问左子树
然后访问右子树

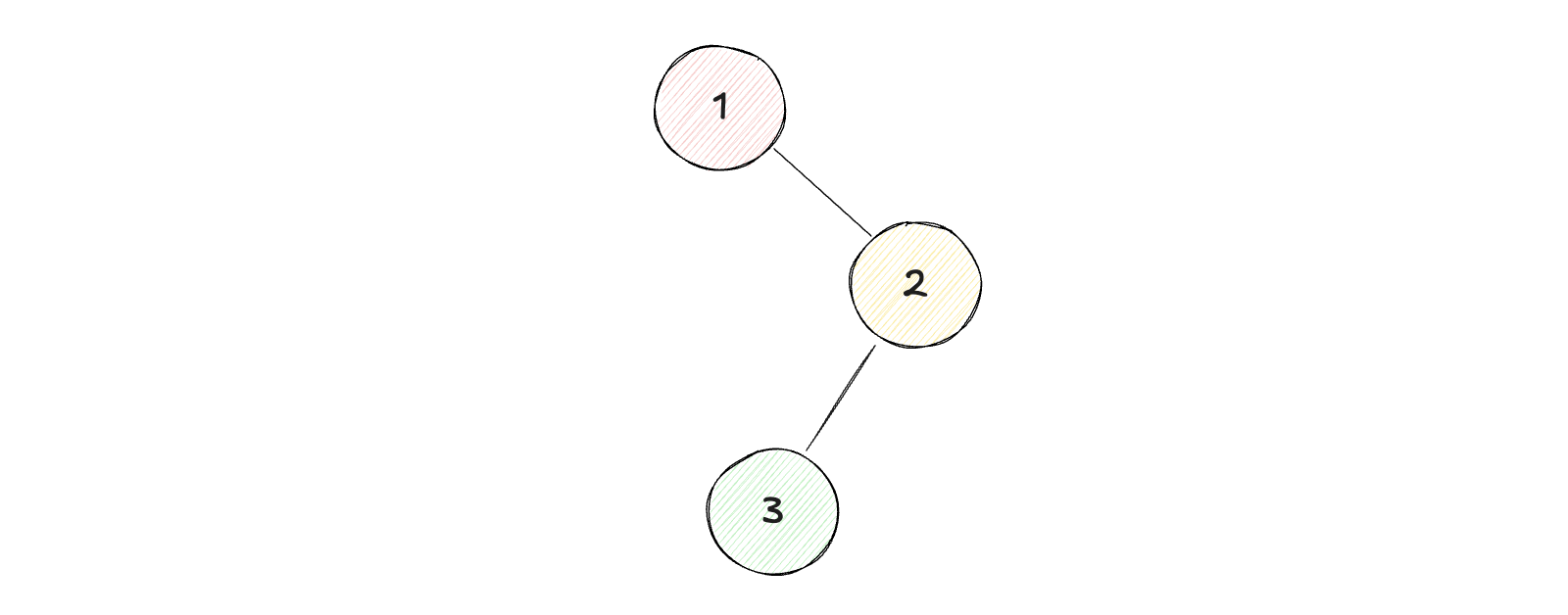
示例1：

index.ts

1输入：root = [1, null, 2, 3]
2输出：[1, 2, 3]

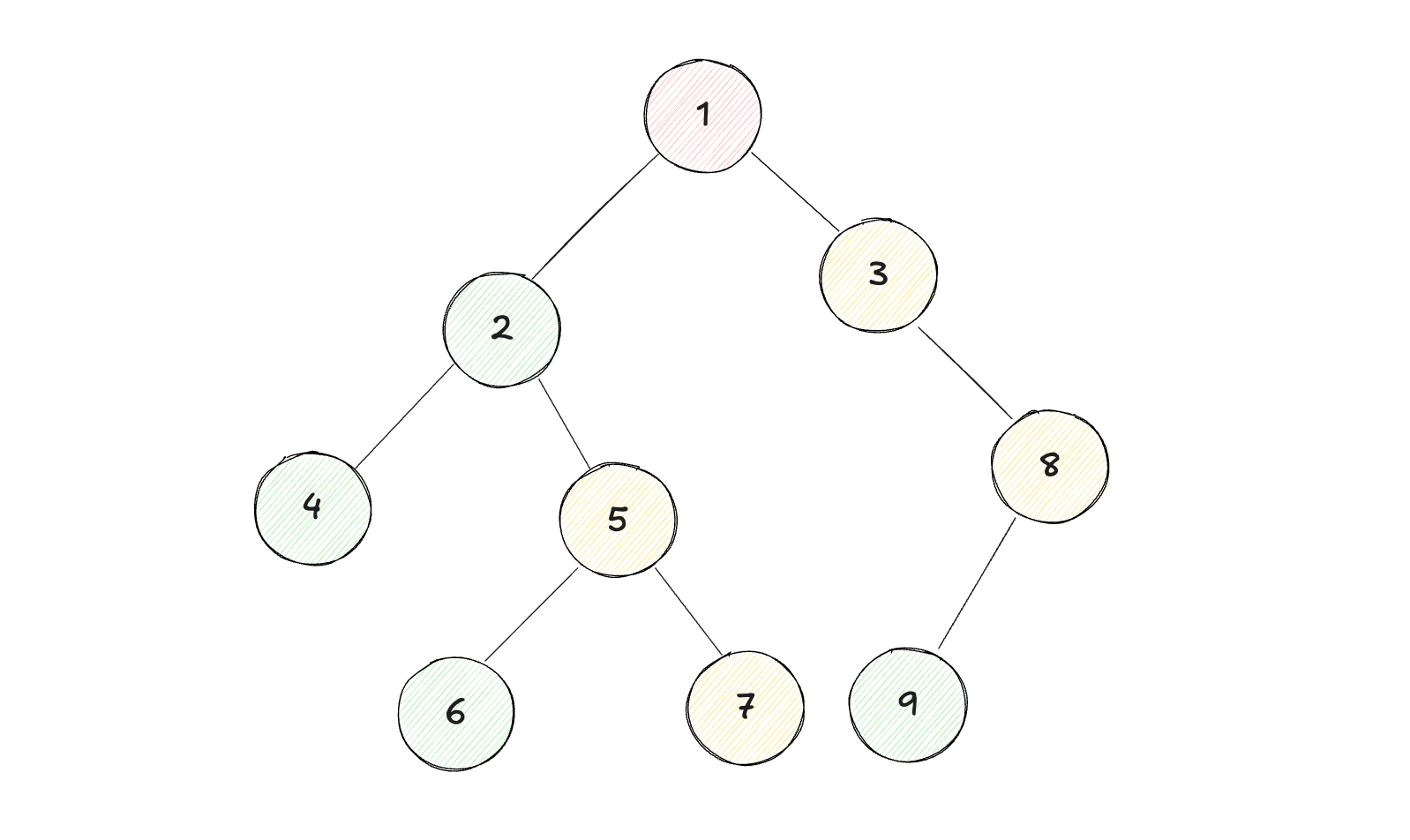
示例2：

index.ts

1输入：root = [1, 2, 3, 4, 5, null, 8, null, null, 6, 7, 9]
2输出：[1, 2, 4, 5, 6, 7, 3, 8, 9]

解题思路

虽然我们不能使用递归来解决这个问题, 但是我们可以使用递归来思考这个问题. 这里其实非常简单, 就是一个深度优先遍历的过程, 遍历的过程中, 把节点值记录到数组中即可

因此, 我们需要首先定义一个数组来收集节点值

index.ts

1// 迭代值
2const res: number[] = []

然后我们继续思考, 如果我们用递归来解决这个问题, 那么我们只需要在递归的过程中, 把节点值记录到数组中即可.

递归思路的完整代码如下所示：

index.ts

01function preorderTraversal(root: TreeNode | null): number[] {
02  const res: number[] = []
03  // 定义递归函数
04  const dfs = (node: TreeNode | null) => {
05    // 如果节点为空, 则直接返回
06    if (!node) {
07      return
08    }
09    // 记录节点值
10    res.push(node.val)  
11    // 递归访问左子树
12    dfs(node.left)
13    // 递归访问右子树
14    dfs(node.right)
15  }
16  // 执行从根节点开始递归
17  dfs(root)
18  return res
19}

通常情况下, 递归、与栈、迭代是相辅相成的. 因此, 当我们在代码规律中, 或者在树形结构中, 没有找到特别明显的起始条件时, 我们可以考虑使用栈来模拟递归的过程. 从而将递归转化为迭代

所以, 这里我们定义一个栈数组, 用于模拟递归的过程.

index.ts

1// 栈数组
2const stack: TreeNode[] = []

当我们遍历过程中, 如果发现一个新的节点, 那么我们就将这个节点压入栈中. 但是如果我们无法通过该节点找到它的子节点, 那么就表示该节点为叶子节点, 此时需要归, 也就是出栈.

NOTE

二叉树的递归过程, 是一个递过程与归过程交替执行的过程, 也就是函数调用栈的执行过程, 如上图所示. 我们在浏览器中看到的火焰图, 也是用于表示函数调用栈的执行过程, 因此上图和火焰图是非常类似的

代码实现上, 我们在遍历过程中, 根据刚才我们的判断条件, 不断将节点压入栈中, 然后不断出栈, 直到栈为空表示执行结束, 就可以得到最终的结果.

index.ts

01function preorderTraversal(root) {
02    const res = []
03  if (!root) {
04    return res
05  }
06  // 定义栈数组
07  const stack = []
08  // 将根节点压入栈中
09  stack.push(root)
10  res.push(root.val)
11  root.x = true // 标记节点是否已经访问过
12  // 遍历栈, 遍历的结束条件为栈数组被清空
13  while(stack.length !== 0) {
14    const top = stack[stack.length - 1]
15    
16    if (top.left && !top.left.x) {
17      stack.push(top.left)
18      top.left.x = true
19      res.push(top.left.val)
20    } else if (top.right && !top.right.x) {
21      stack.push(top.right)
22      top.right.x = true
23      res.push(top.right.val)
24    } else {
25      stack.pop()
26    }
27  }
28  
29  return res
30};

为了区分节点是否已经访问过, 我们使用了一个 x 属性来标记节点是否已经被访问过, 否则会出现重复访问的情况.

我们也可以用另外一种, 不需要标记的方式来实现, 那就是稍微改造一下入栈出栈的时机.

完整代码如下所示：

answer.ts

01class TreeNode {
02  val: number
03  left: TreeNode | null
04  right: TreeNode | null
05  constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
06    this.val = (val===undefined ? 0 : val)
07    this.left = (left===undefined ? null : left)
08    this.right = (right===undefined ? null : right)
09 }
10}
11
12function preorderTraversal(root: TreeNode | null): number[] {
13  const res: number[] = []
14  if (!root) {
15      return res
16  }
17  // 定义栈数组
18  const stack: TreeNode[] = []
19  // 将根节点压入栈中
20  stack.push(root)
21  // 遍历栈, 遍历的结束条件为栈数组被清空
22  while(stack.length !== 0) {
23    // 遍历时首先让节点直接出栈, 此时是利用了巧妙的方式避免了重复判断, 
24    // 所以最终的执行上与栈的出栈入栈时机有细微差异, 但执行顺序是相同的. 不得不利用这个方式是由于我们没有区分左节点右节点是否已经入栈, 
25    const node = stack.pop()
26    // 如果节点为空, 直接跳过
27    if (!node) {
28      continue
29    }
30    // 记录节点值
31    res.push(node.val)
32    // 注意此时的顺序, 为了保证先 pop 左结点, 所以先压入右结点
33    // 如果右节点存在, 则将右节点压入栈中
34    if (node.right) {
35      stack.push(node.right)
36    }
37    // 如果左节点存在, 则将左节点压入栈中
38    if (node.left) {
39      stack.push(node.left)
40    }
41  }
42  
43  return res
44};

这里需要注意的是：遍历时我们首先让节点直接出栈, 这种方式的入栈与出栈时机与函数调用栈是有细微差异的. 这是由于我们没有区分左节点右节点是否已经入栈, 也没有在数据结构上严格的约定我们应该如何入栈出栈, 所以不得不利用这个方式来避免重复判断. 最终的结果是执行顺序是一致的.

以上图为例, 栈中的变化情况为

index.ts

01栈中的变化情况为
02
03[] // 空栈
04[1] // 根节点入栈
05---
06[] // 循环开始, 根节点出栈, 
07[3, 2] // 并将右、左节点入栈
08---
09[3] // 循环开始, 2 节点出栈, 并将右、左节点入栈
10[3, 5, 4]
11---
12[3, 5] // 循环开始, 4 节点出栈, 无子节点
13---
14[3] // 循环开始, 5 节点出栈
15[3, 7, 6] // 并将右、左节点入栈
16---
17[3, 7] // 循环开始, 6 节点出栈, 无子节点
18---
19[3] // 循环开始, 7 节点出栈, 无子节点
20---
21[] // 循环开始, 3 节点出栈
22[8] // 并将右、左节点入栈
23---
24[] // 循环开始, 8 节点出栈
25[9] // 并将右、左节点入栈
26---
27[] // 循环开始, 9 节点出栈, 无子节点
28---
29循环结束

在 React 中, 也使用类似的方式来迭代的遍历树节点, 但是, React 的数据结构的构造上, 使用了 fiber.child fiber.sibling fiber.return 等指针来限制执行顺序. 因此, React 的迭代遍历树结构, 可以与递归的出栈入栈保持严格一致.

练习题：二叉树的后续遍历

原地地址：145. 二叉树的后序遍历

题目描述：

给你一棵二叉树的根节点 root , 返回其节点值的后序遍历数组.

二叉树的三种遍历方法的考查顺序一致, 只是输出顺序不一样：

前序遍历：遍历到一个节点后, 即刻输出该节点的值, 并继续遍历其左右子树. 输出顺序：根、左、右

中序遍历：遍历到一个节点后, 将其暂存, 遍历完左子树后, 再输出该节点的值, 然后遍历右子树. 输出顺序：左、根、右

后序遍历：考察到一个节点后, 将其暂存, 遍历完左右子树后, 再输出该节点的值. 输出顺序：左、右、根

示例1：

index.ts

1输入：root = [1, null, 2, 3]
2输出：[3, 2, 1]

示例2：

index.ts

1输入：root = [1, 2, 3, 4, 5, null, 8, null, null, 6, 7, 9]
2输出：[4, 6, 7, 5, 2, 9, 8, 3, 1]

解题思路：二叉树的后序遍历

专栏首页

到顶

专栏目录