usehook - 前端码易

code deep_

所有专栏

免费领 30 美元额度

创建时间: 2025-04-13最后更新: 2025-12-22作者: yangbo(96862973d)

NOTE

请勿第一时间看答案, 先自己思考, 思考不出来, 再看答案

思考题：二叉树的最大深度

题目描述

给定一个二叉树 root , 返回其最大深度.

二叉树的最大深度：是指从根节点到最远叶子节点的最长路径上的节点数. 如下图所示的二叉树, 最大深度为 3

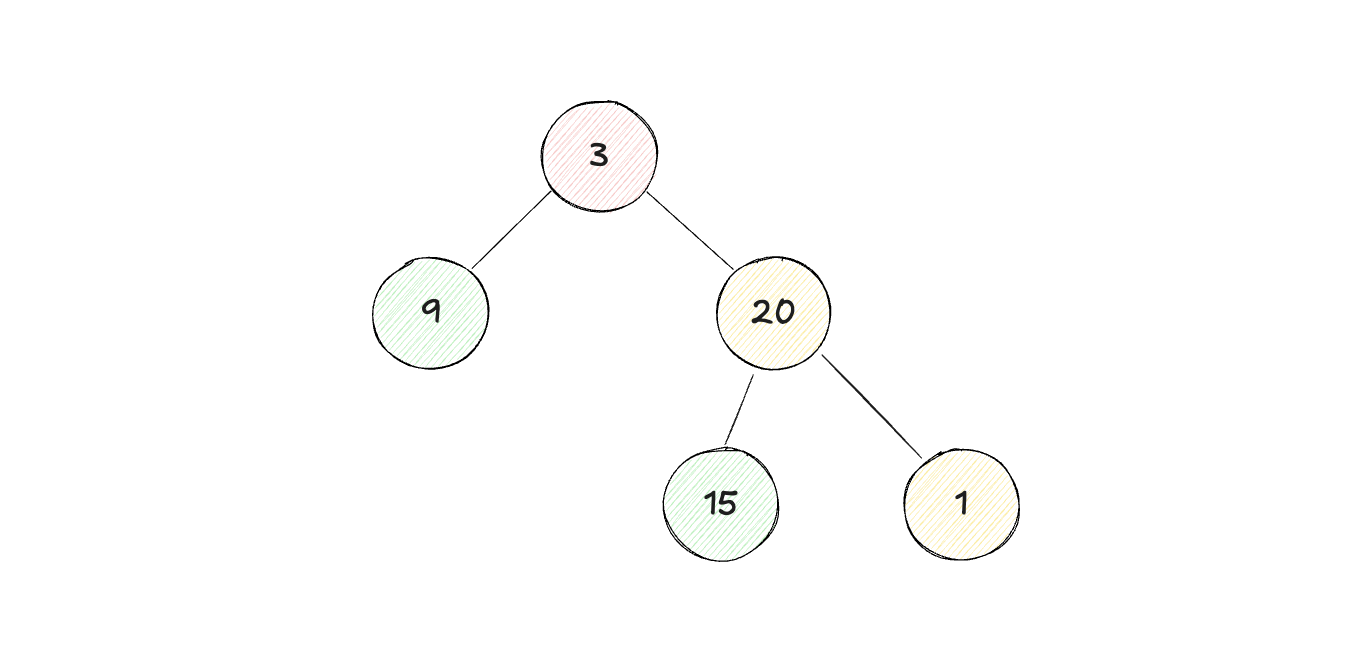
原题地址：leetcode 104

解题思路

使用递归来解题, 主要只关注两个问题

找到规律：如何拆分相同子问题
找到终止条件

我们假定函数 maxDepth(root) 已经可以计算出以 root 为根节点的二叉树的最大深度, 那么, 对于左右两个子节点, 我们会返回值更大的那一边, 所以就有如下关系

code.ts

1Math.max(maxDepth(root.left), maxDepth(root.right))

当然, 每计算一次, 会增加一层, 所以最终的结果应该是

code.ts

1Math.max(maxDepth(root.left), maxDepth(root.right)) + 1

最后我们来思考终止条件. 理论上来说, 当我们找到叶子节点时, 最大深度为 1, 所以我们可以返回 1, 但是由于在上面的规律中, 我们会将左节点与右节点继续传入, 叶子节点的左节点与右节点为空

所以, 终止条件为

code.ts

1if (!root) return 0

完整代码如下

answers.ts

01class TreeNode {
02  val: number
03  left: TreeNode | null
04  right: TreeNode | null
05  constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
06    this.val = (val===undefined ? 0 : val)
07    this.left = (left===undefined ? null : left)
08    this.right = (right===undefined ? null : right)
09 }
10}
11
12export function maxDepth(root: TreeNode | null): number {
13  if (root === null) {
14      return 0
15  }
16  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
17};

专栏首页

到顶

专栏目录