code deep_
创建时间: 2025-06-22最后更新: 2025-12-22作者: yangbo(96862973d)

Table of contents

二分搜索的反向运用

我们通过一个题目来学习这个运用思路.

原题地址：702. 搜索长度未知的有序数组
NOTE

给定一个升序数组 nums, 写一个函数搜索 nums 中的 target, 如果 target 存在返回下标, 否则返回 -1. 注意, 这个数组的大小是未知的, 因此, 我们不能通过数组的长度来计算中间元素的位置. 你只可以通过 ArrayReader 接口来访问数组中的元素.

code.ts
1
interface ArrayReader {

2
  get(index: number): number;

3
}

如果你访问的数组下标越界, ArrayReader 会返回 2^31 - 1.

code.ts
1
const reader = new ArrayReader([-1,0,3,5,9,12]);

2
reader.get(0); // return 0

3
reader.get(3); // return 5

4
reader.get(5); // return 12

5
// 越界

6
reader.get(6); // return 2^31 - 1

解题思路

在上一章中, 我们学习到的二分搜索, 是在数组长度已知的情况下, 对数组进行二分. 但是, 这里的题目是, 我们无法得知数组的长度, 因此, 我们不能通过数组的长度来计算中间元素的位置.

这里, 我们可以通过二分搜索的反向运用, 来尝试性查找大概的数组末尾. 那就是通过放大倍数, 来找到一个可以使用二分搜索的数组末尾. 找到的这个数组末尾可能为空, 但是不影响我们使用二分搜索的算法.

我们图示来演示这个思路

初始状态, 我们设计一个变量 right 来表示数组末尾. 设计一个变量 left 来表示数组起始位置. 初始值为 0 和 1.

code.ts
1
let left = 0;

2
let right = 1;

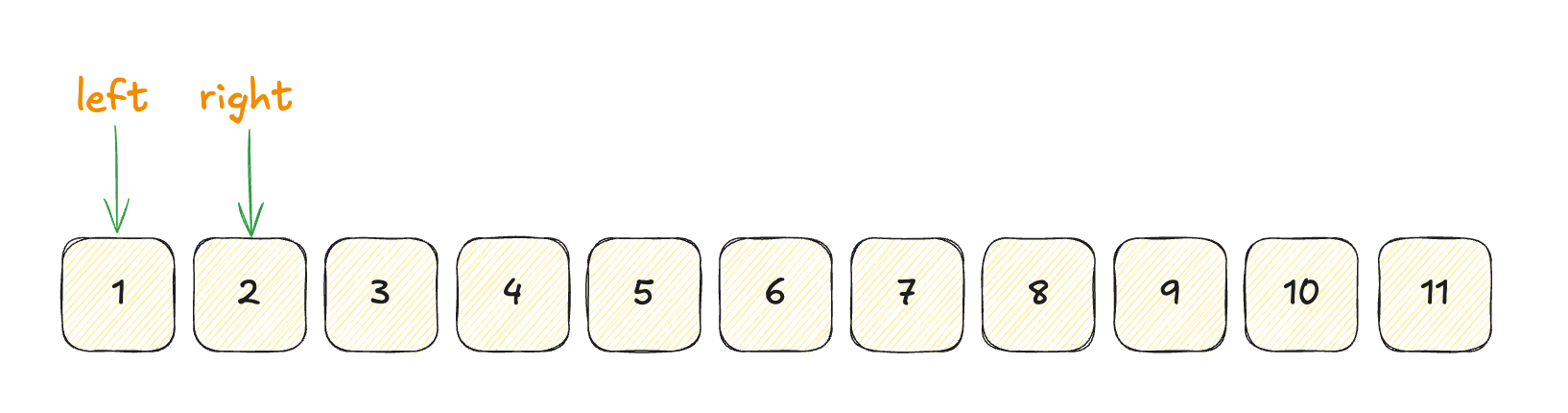
此时, 两个指针共同构成了一个区间数组, 这个区间数组可能包含 target, 也可能不包含 target.

然后我们通过判断 reader.get(right) 是否大于 target 来判断区间数组是否包含 target. 如果还没包含, 则将 right 放大倍数.

code.ts
1
while (reader.get(right) < target) {

2
  right = right * 2;

3
}

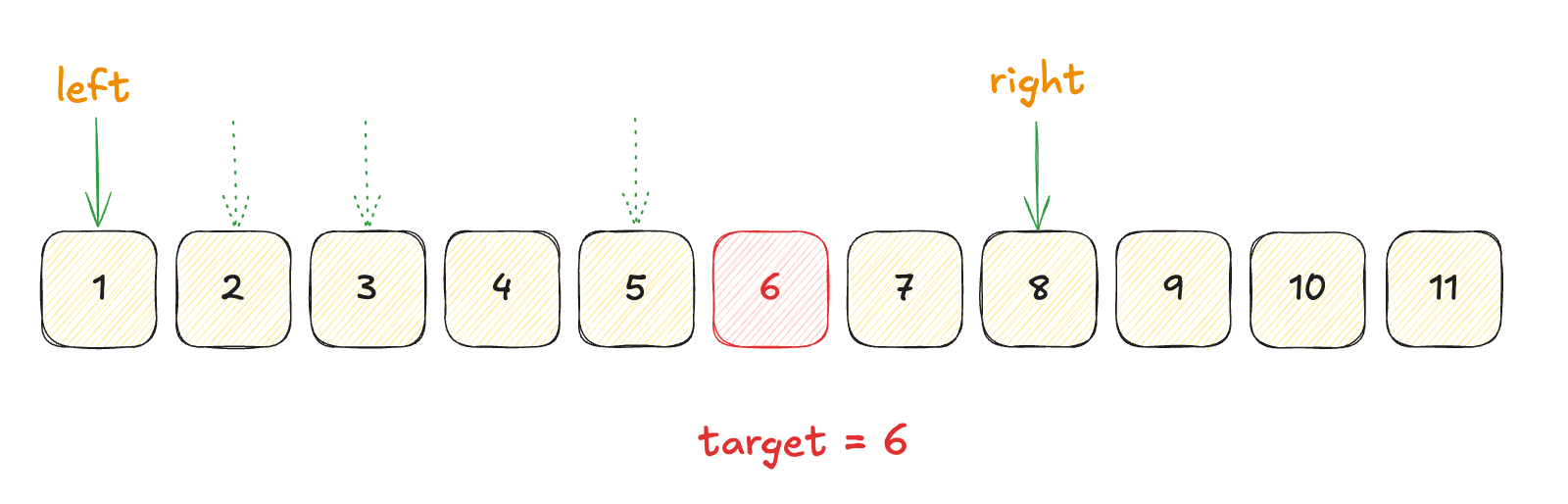
这样, 我们可以快速找到一个必定包含 target 的区间数组. 我们只需要在这个区间数组中, 使用二分搜索, 就可以找到 target 的索引了.

代码实现

完整的代码实现如下所示

search.ts
01
function search(reader: ArrayReader, target: number): number {

02
  let left = 0;

03
  let right = 1;

04
  while (reader.get(right) < target) {

05
    right = right * 2;

06
  }

07
  while (left <= right) {

08
    const mid = Math.floor((left + right) / 2);

09
    const midValue = reader.get(mid);

10
    if (midValue === target) {

11
      return mid;

12
    } else if (midValue < target) {

13
      left = mid + 1;

14
    } else {

15
      right = mid - 1;

16
    }

17
  }

18
  return -1;

19
}

时间复杂度: O(log(n))O(log(n))

空间复杂度: O(1)O(1)

专栏首页
到顶
专栏目录